Vibration control for a backbone structure is achieved by embedment of a periodic or graded lattice whose unit cells include internal resonators and viscoelastic elements. Such internal resonating systems distributed within the base structure are characterized by frequency bands of strong wave attenuation. These “stop-bands” are generated by the out-of-phase motion between the base structure and the locally resonant system, and are centered at the frequencies of internal resonances. Proper tuning of the resonators thus enables vibration cancellation at arbitrarily low frequencies. 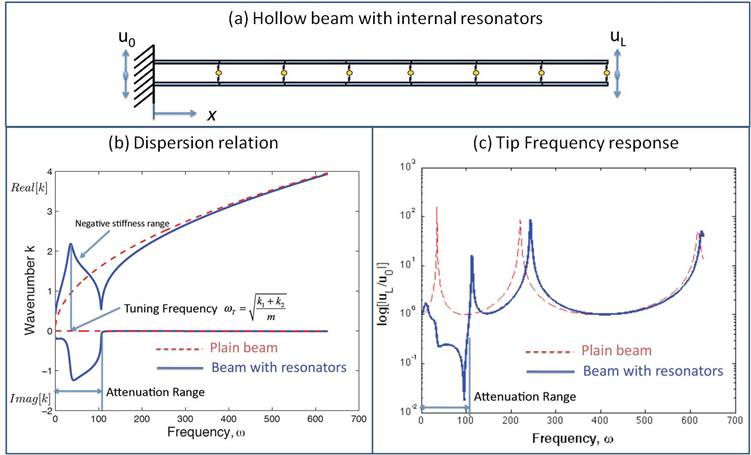This concept is exemplified in Figure 1 below by a structural assembly composed of a hollow beam and internal mass-spring resonators inserted at periodic locations. Figure 1(b) shows the dispersion relation characterizing wave propagation in this periodic structure: a low-frequency attenuation range is generated by the resonators, which is associated with non-zero imaginary part of the dispersion characteristic. The corresponding frequency response function of the beam tip in Figure 1(c) exhibits a wide low-frequency bandgap.
Figure 1: (a) Structural assembly with hollow beam (backbone structure) and internal resonators (lattice inclusions). (b) Dispersion relation for waves propagating in the structure. (c) Frequency response function of the beam tip.
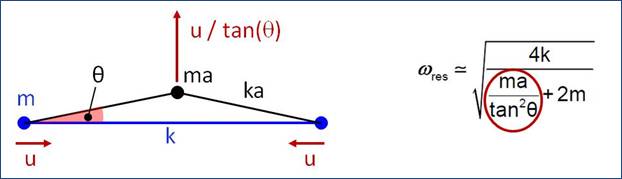
Inertially Amplified Internal Resonator (IAIR) One of the considered implementations of internal resonators exploits the inertial amplification mechanism [1,2] illustrated in Figure 2. The triangular mass-spring system assembly is characterized by a small value of angle θ, whereby small horizontal displacements of base masses m produce large motion of the third mass ma. The resonance frequency of the system is therefore dependent on an effective mass ma / tan^2 θ, which is much greater than the actual mass ma for small values of θ and can be tuned by changing the angle.
Figure 2: IAIR concept: m and ma are masses connected by springs with stiffness k and ka. A horizontal displacement u of base masses m produces enhanced motion u / tanθ of mass ma. An approximate expression of the resonant circular frequency [1] is also indicated.
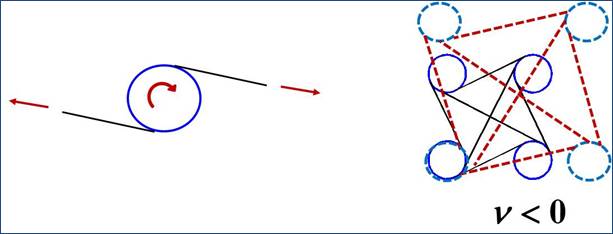
Chiral assemblies Another interesting possibility for the design of internally resonating lattices is to exploit non-central forces acting on stiff ring-shaped components at nodal positions through ligaments attached at suitable locations and angles along the circumference of such elements. As illustrated in Figure 3, compression/stretching applied to the ligaments in one direction will produce a rotation of the ring, causing a similar compression/stretching to be transmitted to ligaments attached at other directions. As a result, such a chiral lattice configuration [3] exhibits negative Poisson’s ratio. Resonating masses can be embedded into the rings and combined with a viscoelastic matrix to provide two-phase assemblies with non-usual material properties, possibly allowing for extreme values of stiffness and damping to be achieved simultaneously.
Figure 3: Application of non-central force concepts to the design of a chiral unit cell with negative Poisson’s ratio ν.
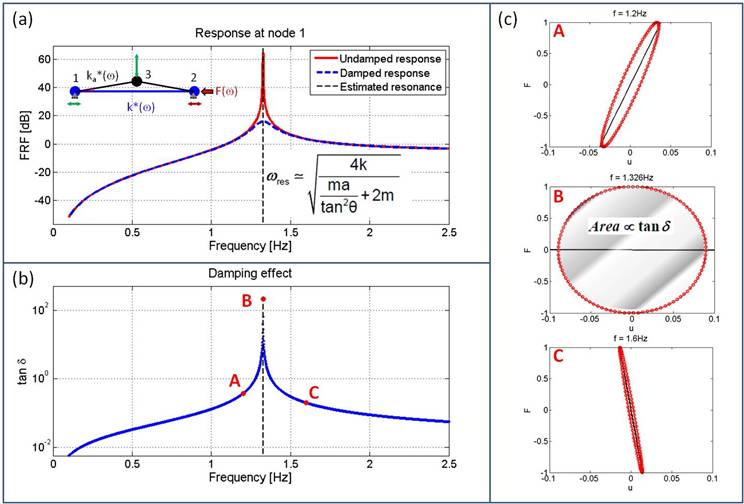
Viscoelastic damping for a structural assembly Viscoelastic damping is typically evaluated in terms of the loss tangent tan δ, where angle δ is the phase lag between stress and strain in the presence of viscous components. For structural assemblies, the loss tangent is determined not only by material properties of the constituents, but also by the geometry of the structure [4]. Embedding viscoelastic elements into resonator configurations described above thus provides an interesting opportunity for effective dissipation of the energy pumped away from the backbone structure at local resonances. An example is illustrated in Figure 4 below with reference to an IAIR cell with viscoelastic spring elements. Figure 4(a) shows the damping effect produced in the frequency response by the introduction of viscoelastic components: maximum dissipation occurs at the resonance frequency, as confirmed by the peak in loss tangent (Figure 4(b)) and by hysteresis curves in Figure 4(c). The area enclosed by these curves is an indication of the amount of losses occurring in the system, and it is maximized in resonance conditions.
Figure 4: (a) Frequency response of an IAIR cell with simply elastic (red line) or viscoelastic spring elements (blue line). (b) Corresponding loss tangent for the viscoelastic cell. (c) Hysteresis force-displacement curves showing dissipation at different frequencies (associated with points A, B, and C in plot (b), respectively).
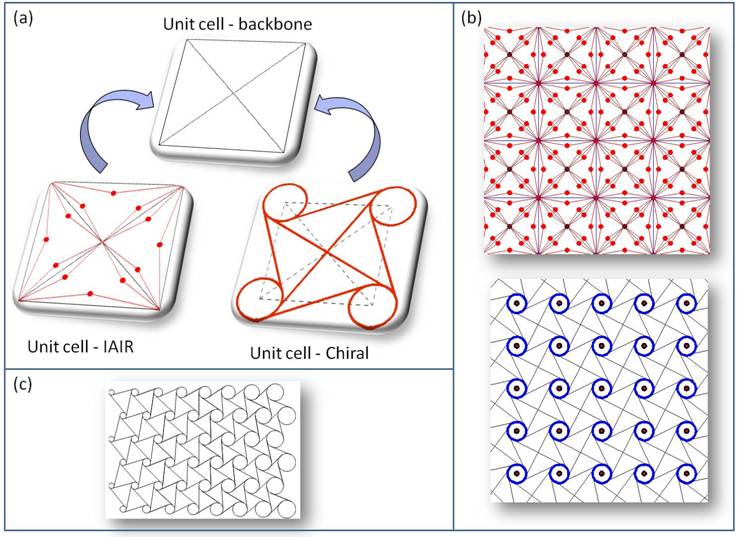
Lattice and graded configurations The concepts outlined above can be integrated into a backbone structure by defining unit cells with suitable resonant configurations and arranging them into structural lattices through a modular approach. Sample IAIR and chiral unit cells are shown in Figure 5(a), along with resulting lattice assemblies in Figure 5(b). The presence of multiple degrees of freedom within these resonant systems broadens the frequency range in which vibration cancellation can be achieved. Even wider bandwidths can be obtained by using graded configurations such as the one sketched in Figure 5(c).
Figure 5: (a) Design of IAIR and chiral unit cells starting from a backbone element. (b) IAIR and chiral lattice assemblies. (c) Graded chiral configuration.
References [1] C. Yilmaz, G. M. Hulbert, N. Kikuchi, “Phononic band gaps induced by inertial amplification in periodic media”, Physical Review B 76 (2007), pp. 054309-1 - 054309-9. [2] C. Yilmaz, G. M. Hulbert, “Theory of phononic gaps induced by inertial amplification in finite structures”, Physics Letters A 374 (2010), pp. 3576-3584. [3] A. Spadoni, M. Ruzzene, S. Gonella, F. Scarpa, “Phononic characteristics of hexagonal chiral lattices, Wave Motion 46:7 (2009), pp. 435-450. [4] Y.-C. Wang, J. G. Swadener, R. S. Lakes, “Two-dimensional viscoelastic discrete triangular system with negative-stiffness components”, Philosophical Magazine Letters 86:2 (2006), pp. 99-112.
Georgia Institute of Technology – School of Aerospace Engineering Atlanta, Georgia 30332-0150 Contact Us:
Massimo Ruzzane Emanuele Baravelli	ruzzene@gatech.edu ebaravelli@gatech.edu